A 'logical Bell inequality' for qubit phase space

This is a sort of appendix to a blog post I’m writing, and will make a lot more sense with that context. I want to find stationary points of the sum of marginal probabilities \(\sum p_i = p_z + p_x + p_y\), where the \(p_i\)s are defined as in my qubit phase space cheat sheet:

\(\sum p_i = \frac{3}{2} - \frac{1}{2}(\cos\theta + \sin\theta\cos\phi + \sin\theta\sin\phi)\),

where \(\theta \in [0, \pi ]\) and \(\phi \in [0, 2\pi )\).

The rest of this page is just the details of finding and classifying the stationary points, which occur when:

1. \(\frac{\partial \sum p_i}{\partial \phi} = 0\) and
2. \(\frac{\partial \sum p_i}{\partial \theta} = 0\).

The details are in the next section, then there’s a summary and graphs, then I find the corresponding qubit states.

Details

Equation 1. gives

\(\sin \theta \sin \phi = \sin \theta \cos \phi\).

So either:

• \(\sin\theta = 0\), so that \(\theta = 0, \pi\)
• \(\sin\phi = \cos\phi\), so that \(\phi = \frac{\pi}{4}, \frac{5\pi}{4}\).

Deal with the \(\sin\theta = 0\) case first. In that case \(\sum p_i\) just becomes a constant. At \(\theta = 0\), \(\sum p_i = \frac{3}{2} - \frac{1}{2} = 1\), and at \(\theta = \pi\), \(\sum p_i = \frac{3}{2} + \frac{1}{2} = 2\). So there are lines of constant \(\sum p_i\) at these values of \(\theta\).

Then take the remaining \(\sin\phi = \cos\phi\) case, and apply equation 2 as well:

\(\cos\theta\cos\phi + \cos\theta\sin\phi = \sin\theta\),

or (as \(\cos\theta \neq 0\) at any of the stationary points)

\(\cos\phi + \sin\phi = \tan\theta\).

At \(\phi = \frac{\pi}{4}\), \(\tan\theta = \sqrt{2}\), so

\(\sin\theta = \frac{\sqrt{2}}{\sqrt{3}}\) and \(\cos\theta = \frac{1}{\sqrt{3}}\)

This happens when \(\sum p_i = \frac{1}{2}(3 - \sqrt{3}) \sim 0.634\).

At \(\phi = \frac{5\pi}{4}\), \(\tan\theta = -\sqrt{2}\), so

\(\sin\theta = \frac{\sqrt{2}}{\sqrt{3}}\) and \(\cos\theta = -\frac{1}{\sqrt{3}}\)

This happens when \(\sum p_i = \frac{1}{2}(3 + \sqrt{3}) \sim 2.366\).

Summary

• Maximum line at \(\theta = \pi\), value \(\sum p_i = 2\)
• Minimum line at \(\theta = 0\), value \(\sum p_i = 1\)
• Maximum point at \(\phi = \frac{5\pi}{4}\), \(\sin\theta = \frac{\sqrt{2}}{\sqrt{3}}\), \(\cos\theta = -\frac{1}{\sqrt{3}}\), value of \(\sum p_i = \frac{1}{2}(3 + \sqrt{3})\)
• Minimum point at \(\phi = \frac{\pi}{4}\), \(\sin\theta = \frac{\sqrt{2}}{\sqrt{3}}\), \(\cos\theta = \frac{1}{\sqrt{3}}\), value of \(\sum p_i = \frac{1}{2}(3 - \sqrt{3})\).

The last one is the case we’re really interested in, as we want to maximise \(\sum p_i\). Will find the corresponding qubit state below.

Overall the function \(\sum p_i\) looks like this (thanks WolframAlpha):

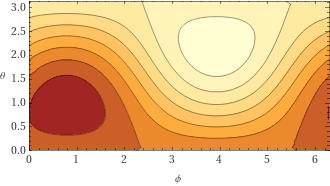
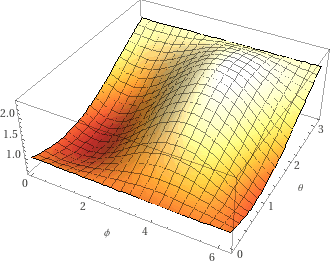
The qubit phase space state for the maximum point is the following: